传感器的响应时间

关于响应时间，例如热电偶测量水温的实验过程：

1. 用恒温水槽，水温 $T$，环境温度 $T_0$ ，热电偶首先处于外部环境中，稳定后，反映环境温度 $T_0$；
2. 将热电偶迅速插入到恒温水槽中，这时候热电偶感受的温度参数发生突变，由 $T_0$ 到 $T$。

那么此时，热电偶输出反映的温度就是 $T$ 吗？答案通常情况之下是否定的，通常可以看到热电偶反映的温度有一个逐渐上升的过程，最终会达到 $T$。而这样的一个过程就是热电偶动态特性的一个体现，如图所示：

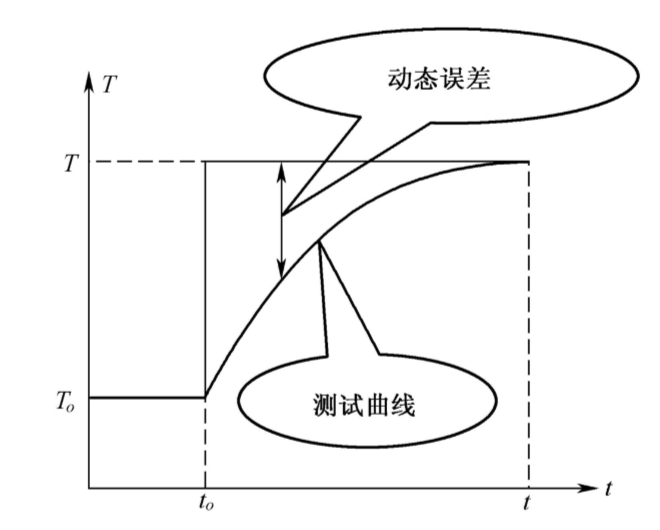
温度的突变是阶跃输入。如果传感器的动态特性足够好的话，那么传感器的输出也应该是一个阶跃输出，但上面的例子中热电偶总是需要一定的时间才能够指示出正确的温度，动态特性越好的热电偶，需要的时间会越短；而在特定时刻，热电偶示出的温度与真实的恒温水槽温度之间的差别就是某时刻的动态误差，这是与时间因素相关的误差。

响应时间是指从输入量开始起作用到输出指示值进入稳定值所规定的范围内所需要的时间。这个时间与规定的范围有关，这个时间意味着，从这个时间之后输出指示值将全部落在规定的范围之内。

对于一般情况，当传感器输入一个单位阶跃信号时，其输出信号称为阶跃响应。传感器常见的一阶及二阶阶跃响应曲线如图所示：

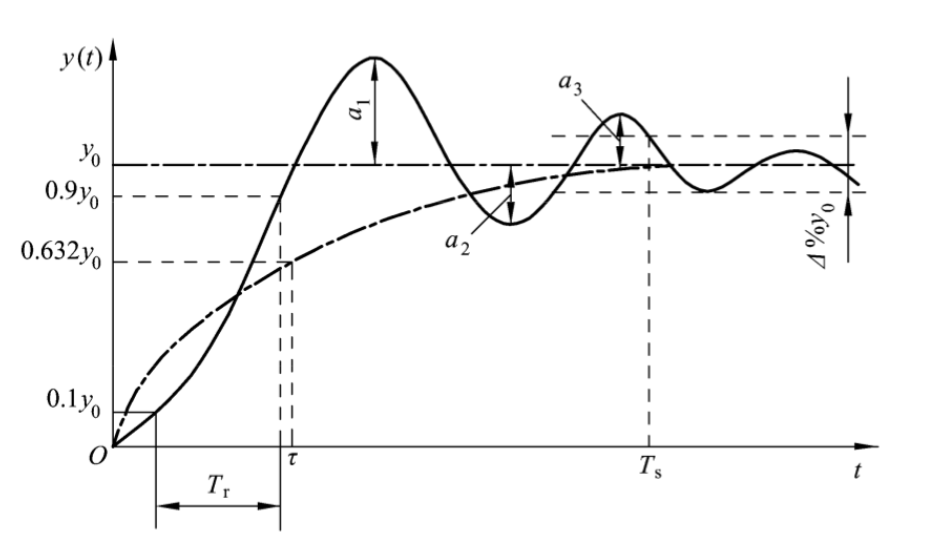
主要的特性指标如下：

1. 时间常数 $τ$ 为一阶传感器输出值上升到稳态值的 63.2% 所需的时间。它是描述一阶传感器动态特性的重要参数，$τ$ 越小，响应速度越快；
2. 上升时间 $T_r$ 为传感器输出值由稳态值的 10% 上升到 90% 所需的时间，但有时也规定其他百分数；
3. 响应时间 $T_s$ 为系统从阶跃输入开始到输出值进入稳态值所规定的范围内所需的时间。一般在稳态响应值 $y_0$ 的上下规定一个 $\pm\Delta%$ 的公差带，当响应曲线开始全部进入这个公差带的时刻就是响应时间 $T_s$。为了明确起见，往往说“百分之 $\Delta$ 响应时间”。

通常使用两个不同指标来定义响应时间：$T_{63}$ 和 $T_{90}$。当被测参数量值有瞬时变化时，测量值需要多长时间达到最终值的 63% 或 90%。

以下是为什么选择 63% 来定义响应时间的原因：$T_{63}$ 在一阶线性时域不变系统中等于时间常数 $τ$。这个一阶线性时域不变系统的数学模型描述了某一物理系统对阶跃变化呈指数曲线的反应，如图。这意味着系统将在一个时间常数内达到最终值的 63%，在三个时间常数内达到最终值的 95%，在四个时间常数内达到最终值的 98%。

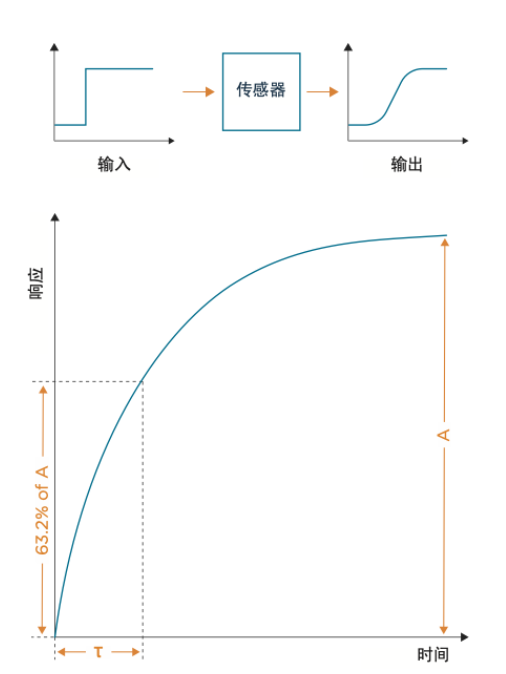
一般认为，阶跃输入对于一个传感器来说是最严峻的工作状态。如果在阶跃函数的作用下，传感器能满足动态性能指标，那么在其他函数作用下，其动态性能指标也必定会令人满意。